Signals and Systems Exam Questions and Solutions

The value of \(\mathop \smallint \limits_{ - \infty }^{ + \infty } {e^{ - t}}\delta \left( {2t - 2} \right)dt\), where \(\delta \left( t \right)\) is the Dirac delta function, is

1. \(\frac{1}{{2e}}\)
2. \(\frac{2}{e}\)
3. \(\frac{1}{{{e^2}}}\)
4. \(\frac{1}{{2{e^2}}}\)

Answer (Detailed Solution Below)

Option 1 : \(\frac{1}{{2e}}\)

Concept :

• Shifting property of impulse function

\(\rm\displaystyle\int_{-\infty}^{\infty} x(t) \delta (t -a ) dt = x(a)\)

• Scaling property of impulse function

\(\delta (at) = \frac{1}{|a|)} \delta (t)\)

Explanation :

Let,

\(\rm I =\displaystyle\int_{-\infty}^{\infty}e^{-t} \delta(2t - 2) dt\)

\(\Rightarrow I = \rm\displaystyle\int_{-\infty}^{\infty}e^{-t} \delta[2(t - 1)] dt\)           {By scaling property of impulse function}

\( \Rightarrow I =\rm\displaystyle\int_{-\infty}^{\infty}e^{-t} \frac{1}{|2|}\delta(t - 1) dt\)

\(\Rightarrow I =\frac{1}{2}\rm\displaystyle\int_{-\infty}^{\infty}e^{-t} \delta(t - 1) dt\)             {By shifting property of impulse function}

\(\Rightarrow I = \frac{1}{2}. \left. e^{-t} \right|_{t = 1}\)

\(\Rightarrow I = \frac{1}{2e}\)

News Around the World

Find out even and odd part of signal x(t) = (2 + sin t)²

1. 4 + sin²t, 4 sin t
2. 2 + sin²t, 2 sin t
3. 4, 4 sin t + sin² t
4. 2, sin t

Answer (Detailed Solution Below)

Option 1 : 4 + sin²t, 4 sin t

Concept:

Any given signal x(t) can be written as the sum of its even part and odd part, i.e.

x(t) = xe(t) + xo(t)

xe(t) = Even part of g(t) calculated as:

\(x_e(t)=\frac{x(t)+x(-t)}{2}\)

xo(t) = Odd part of x(t) calculated as:

\(x_o(t)=\frac{x(t)-x(-t)}{2}\)

Calculation :

Given:

x(t) = (2 + sin t)²

x(t) = 4 + sin²t + 4 sin t

x(-t) = 4 + sin2t - 4 sin t

Even part of g(t) calculated as:

\(x_e(t)=\frac{x(t)+x(-t)}{2}\)

\(=\frac{4+sin^2⁡t+4 sin⁡t+4+sin^2⁡t-4 sin⁡t }{2}\)

= 4 + sin2t

Odd part of x(t) calculated as:

\(x_o(t)=\frac{x(t)-x(-t)}{2}\) \(\)

\(=\frac{4+sin^2⁡t+4 sin⁡t-4-sin^2⁡t+4 sin⁡t }{2}\)

= 4 sin t

Which of the following is false for a continuous time signal?

1. Any signal can be expressed as the sum of an odd and an even signals
2. Sum of two periodic signals is always periodic
3. Any periodic signal can be expressed as sum of sinusoidal signals
4. None of the above

Answer (Detailed Solution Below)

Option 2 : Sum of two periodic signals is always periodic

Even and odd property:

Any given signal g(t) can be written as the sum of its even part and odd part, i.e.

g(t) = ge(t) + go(t)

ge(t) = Even part of g(t) calculated as:

\(g_e(t)=\frac{g(t)+g(-t)}{2}\)

go(t) = Odd part of g(t) calculated as:

\(g_o(t)=\frac{g(t)-g(-t)}{2}\)

Periodicity of sum two periodic signals:

A signal x(t) is said to be periodic if for some positive constant T0;

x(t) = x (t + T0) for all t

The smallest value of T0 that satisfies the periodicity condition of the above equation is called the fundamental period of x(t).

The sum of two periodic functions is often periodic, but not always.

Suppose that x(t) is periodic with fundamental period P, and g(t) is periodic with fundamental period Q. Then x(t) + g(t) will be periodic with a period R, if P and Q both have a common multiple R.

Ex- sin x + sin πx

sin x is periodic with a period 2π

sin πx is periodic with a period 2

But since 2π and 2 have no common multiple, the sum of the two signals will not be periodic.

Fourier Series:

Fourier series states that any periodic signal x(t) can be expressed as the sum of the sinusoidal signals.

Mathematically, it is defined as:

\(x\left( t \right) = {A_0} + \mathop \sum \limits_{n = 1}^{n = \infty } ({A_n}cosn{\omega _0}t + {B_n}\sin n{\omega _0}t)\)

An unit impulse function in continuous form is defined to be

1. δ(t) = t
2. δ(t) = 1
3. \(\delta \left( t \right) = \left\{ {\begin{array}{*{20}{c}} {\infty ,\;\;t = 0}\\ {0,\;\;t \ne 0} \end{array}} \right.\)
4. \(\delta \left( t \right) = \left\{ {\begin{array}{*{20}{c}} {0,\;\;t = 0}\\ {1,\;\;t \ne 0} \end{array}} \right.\)

Answer (Detailed Solution Below)

Option 3 : \(\delta \left( t \right) = \left\{ {\begin{array}{*{20}{c}} {\infty ,\;\;t = 0}\\ {0,\;\;t \ne 0} \end{array}} \right.\)

Unit impulse function:

It is defined as

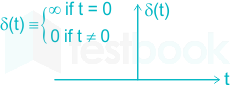
Properties:

1.\(\mathop \smallint \limits_{ - \infty }^\infty \delta \left( t \right)dt = 1\)

2.\(\delta \left( {at} \right) = \frac{1}{{\left| a \right|}}\delta \left( t \right)\)

3. x(t) δ(t – t0) = x(t0)

4.\(\mathop \smallint \limits_{ - \infty }^\infty x\left( t \right)\delta \left( {t - {t_o}} \right)dt = x\left( {{t_0}} \right)\)

5.\(\mathop \smallint \limits_{ - \infty }^\infty f\left( t \right)\delta \left( {at + b} \right)dt = \mathop \smallint \limits_{ - \infty }^\infty f\left( t \right)\frac{1}{{\left| a \right|}}\delta \left( {t + \frac{b}{a}} \right)dt\)

6.\(\mathop \smallint \limits_{ - \infty }^\infty x\left( t \right){\delta ^n}\left( {t - {t_o}} \right)dt = {\left. {\frac{{{d^n}x}}{{d{t^n}}}} \right|_{t = {t_0}}}\)

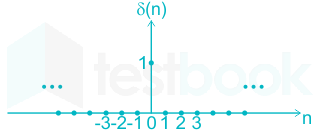
The discrete time version of the unit impulse is defined by

\(\delta \left[ n \right] = \left\{ {\begin{array}{*{20}{c}} {1,\;\;n = 0}\\ {0,\;\;n \ne 0} \end{array}} \right.\)

Properties:

1. x[n] δ[n] = x[0] δ[n]

2.\(\mathop \sum \limits_{n = - \infty }^{n = \infty } x\left[ n \right]\delta \left[ n \right] = \mathop \sum \limits_{n = - \infty }^{n = \infty } x\left[ 0 \right]\delta \left[ n \right] = x\left[ 0 \right]\)

3. x[n] δ[n – n0] = x[n0] δ[n – n0]

4.\(\mathop \sum \limits_{n = - \infty }^{n = \infty } x\left[ n \right]\delta \left[ {n - {n_0}} \right] = \mathop \sum \limits_{n = - \infty }^{n = \infty } x\left[ {{n_0}} \right]\delta \left[ {n - {n_0}} \right] = x\left[ {{n_0}} \right]\)

5. δ[an] = δ[n]

Identify the nature of the signal shown in the given image.

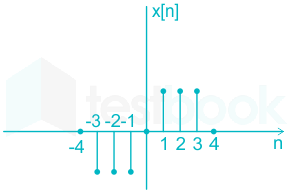
1. Odd signals
2. Periodic signals
3. Even signals
4. Aperiodic signals

Answer (Detailed Solution Below)

Option 1 : Odd signals

Odd Signals:

• A signal x(t) is said to be an odd signal if it satisfies the condition:

          x(-t) = - x(t) for all t (Continuous Time)

          x(-n) = - x(n) for all n(Discrete Time)

• An odd signal is anti symmetrical about the vertical axis.

Analysis:

Fro the given signal, we can write:

x[-n] = - x[n]

∴ The given signal x[n] is an odd signal.

Examples of odd signals:

Even Signals:

• Any signal x(t) is said to be an even signal if it satisfies the condition:

          x(-t) = x(t) for all t(Continuous Time)

          x(-n) = x(n) for all n(Discrete Time)

• An even signal is identical to its time-reversed signal, i.e. it is symmetrical around the vertical axis.

Examples of even signals:

If a signal f(t) has energy E, the energy of the signal f(2t) is equal to

1. E
2. E/2
3. 2E
4. 4E

Answer (Detailed Solution Below)

Option 2 : E/2

Concept:

If the energy of signal x(t) is E then

The energy of signal Ax(Bt + c) is\(\frac{{{A}^{2}}E}{\left| B \right|}\)

Calculation:

Comparing with the standard equation

A = 1

B = 2

C = 0

Energy of y(t)\(=\frac{{{A}^{2}}E}{\left| B \right|}\)

\(=\frac{E}{2}\)

Hence, option 2 is correct.

The fourth harmonic of a fundamental frequency is 512 Hz. What is the fundamental frequency?

1. 256 Hz
2. 126 Hz
3. 102.4 Hz
4. 128 Hz

Answer (Detailed Solution Below)

Option 4 : 128 Hz

Concept:

Fundamental frequency : Fundamental frequency is theminimumfrequency of vibration.

nth harmonic of the fundamental frequency is given as:

n^th harmonic = n x fundamental frequency

\(f_0=\frac{n^{th} \ Harmonic}{n}\)

Calculation:

Given:

n = 4, 4th harmonic = 512 Hz

∴ The fundamental frequency (f₀) will be:

\(f_0=\frac{n^{th} \ Harmonic}{n}=\frac{512}{4}\)

f₀ = 128 Hz

Consider a signal x(t) = 2r(t) – 2r(t - 2) – 4u(t - 4), evaluate\(\mathop \smallint \limits_{ - \infty }^\infty x\left( t \right)\delta \left( {t - 3} \right)\)

1. 3
2. 4
3. 0
4. -4

Answer (Detailed Solution Below)

Option 2 : 4

Concept:

Sampling property of impulse function is:

\(\mathop \smallint \limits_{{t_1}}^{{t_2}} x\left( t \right)\delta \left( {t - {t_0}} \right) = x\left( {{t_0}} \right)\;\;;\;\;{t_1} < {t_0} < {t_2}\)

Unit ramp function is defined as:

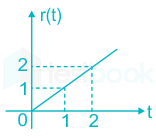
\(r\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {t\;\;;\;\;\;t > 0}\\ {0;\;\;\;\;t < 0} \end{array}} \right\}\)

Calculation:

Given:

x(t) = 2r(t) – 2r (t - 2) – 4u(t - 4)

from sampling property;

\(\mathop \smallint \limits_{ - \infty }^{ + \infty } x\left( t \right)\delta \left( {t - 3} \right) = x\left( 3 \right)\)

So,

x(3) = 2r(3) – 2r(1) – 4u(-1)

x(3) = 2 × 3 – 2 × 1 – 4 × 0

x(3) = 4

Match List-I with List-II and select the correct answer using the code given below the Lists:

List - I	List – II
A. Even signal	1.\((\frac{1}{4})^{n} ~u(n)\)
B. Casual signal	2. x(-n) = x(n)
C. Periodic signal	3. x(t) u(t)
D. Energy signal	4. x(n) = x(n + N)

1. A – 2, B – 3, C – 4, D - 1
2. A – 1, B – 3, C – 4, D - 2
3. A – 2, B – 4, C – 3, D - 1
4. A – 1, B – 4, C – 3, D - 2

Answer (Detailed Solution Below)

Option 1 : A – 2, B – 3, C – 4, D - 1

Even signal:

• Any signal g(t) is said to be an even signal if it satisfies the condition.
•  g (t) = g (-t) for all t
• An even signal is identical to its time-reversed signal, i.e. it is symmetrical around the vertical axis.

Causal signal:

• Causal Signals  are signals  that are zero for all negative time.
• x(t) = 0 for t < 0

​Periodic signals:

• Periodic signals are ones that repeat itself after a regular interval of time.
• x(n) = x(n+N) and x(t) = x(t+T)

​Energy signals:

• Energy signals are one that has finite energy.
• The energy of a signal is defined as the area under the squared magnitude of the signal.
• \(E = \begin{array}{*{20}{c}} {lim}\\ {N \to \infty } \end{array}\mathop \sum \limits_{ - N}^N {\left( {u\left[ n \right]} \right)^2} = \infty \)

Analysis:

The energy of\((\frac{1}{4})^{n} ~u(n)\) can be calculated as follows:

\(E = \begin{array}{*{20}{c}} {lim}\\ {N \to \infty } \end{array}\mathop \sum \limits_{0}^\infty(\frac{1}{4})^{2n}\)

= 16/15 J

∴ Based on the definition we can see that the correct option is 1.

If x(-t) = x(t), x[-n] = x[n] then signals x(t) and x[n] are called as ______

1. non-periodic signal
2. periodic signal
3. odd signal
4. even signal

Answer (Detailed Solution Below)

Option 4 : even signal

Even Signals:

• Any signal x(t) is said to be an even signal if it satisfies the condition:

          x(-t) = x(t) for all t(Continuous Time)

          x(-n) = x(n) for all n(Discrete Time)

• An even signal is identical to its time-reversed signal, i.e. it is symmetrical around the vertical axis.

Examples of even signals:

Odd Signals:

• A signal x(t) is said to be an odd signal if it satisfies the condition:

          x(-t) = - x(t) for all t(Continuous Time)

          x(-n) = - x(n) for all n(Discrete Time)

• An odd signal is anti symmetrical about the vertical axis.

Examples of odd signals:

Evaluate \(\mathop \smallint \limits_{ - \infty }^\infty {e^{ - t}}\delta \left( {2t - 2} \right)dt\)

1. 0
2. \(\frac{1}{{2e}}\)
3. 1
4. \(\frac{1}{{e}}\)

Answer (Detailed Solution Below)

Option 2 : \(\frac{1}{{2e}}\)

Unit impulse function:

It is defined as,\(\delta \left( t \right) = \left\{ {\begin{array}{*{20}{c}} {\infty ,\;\;t = 0}\\ {0,\;\;t \ne 0} \end{array}} \right.\)

The discrete-time version of the unit impulse is defined by

\(\delta \left[ n \right] = \left\{ {\begin{array}{*{20}{c}} {1,\;\;n = 0}\\ {0,\;\;n \ne 0} \end{array}} \right.\)

Properties:

1.\(\mathop \smallint \limits_{ - \infty }^\infty \delta \left( t \right)dt = 1\)

2.\(\delta \left( {at} \right) = \frac{1}{{\left| a \right|}}\delta \left( t \right)\)

3. x(t) δ(t – t0) = x(t0)

4.\(\mathop \smallint \limits_{ - \infty }^\infty x\left( t \right)\delta \left( {t - {t_o}} \right)dt = x\left( {{t_0}} \right)\)

5.\(\mathop \smallint \limits_{ - \infty }^\infty f\left( t \right)\delta \left( {at + b} \right)dt = \mathop \smallint \limits_{ - \infty }^\infty f\left( t \right)\frac{1}{{\left| a \right|}}\delta \left( {t + \frac{b}{a}} \right)dt\)

6.\(\mathop \smallint \limits_{ - \infty }^\infty x\left( t \right){\delta ^n}\left( {t - {t_o}} \right)dt = {\left. {\frac{{{d^n}x}}{{d{t^n}}}} \right|_{t = {t_0}}}\)

Calculation:

\(\mathop \smallint \limits_{ - \infty }^\infty {e^{ - t}}\delta \left( {2t - 2} \right)dt\)

\( = \frac{1}{2}\mathop \smallint \limits_{ - \infty }^\infty {e^{ - t}}\delta \left( {t - 1} \right)dt\)

\( = \frac{1}{2}{e^{ - 1}} = \frac{1}{{2e}}\)

Find the first derivative of the signal.

X(t) = t[u(t) – u(t – a)], a > 0

1. u(t) + u(t – a) – aδ(t –a)
2. u(t) – δ(t – a)- aδ(t – a)
3. u(t) – u(t – a) + aδ(t – a)
4. u(t) – u(t – a) –aδ(t – a)

Answer (Detailed Solution Below)

Option 4 : u(t) – u(t – a) –aδ(t – a)

Concept:

• The derivative of a unit-step function [u(t)] is an impulse function [δ(t)]
• Impulse function =\(\frac{d}{{dt}}\) (Unit step response)
• Unit step function =\(\frac{d}{{dt}}\) (Response of ramp function)
• Ramp function =\(\frac{d}{{dt}}\) (Response of parabolic function)

Calculation:

x (t) = t[u(t) – u(t – a)], a > 0

\(\frac{{dx\left( t \right)}}{{dt}} = t\left[ {{\rm{\delta }}\left( {\rm{t}} \right) - {\rm{\delta }}\left( {{\rm{t}} - {\rm{a}}} \right)} \right] + \left[ {{\rm{u}}\left( {\rm{t}} \right) - {\rm{u}}\left( {{\rm{t}} - {\rm{a}}} \right)} \right] \times 1{\rm{\;}}\)

\(\frac{{dx\left( t \right)}}{{dt}} = \left[ {{\rm{t\delta }}\left( {\rm{t}} \right) - {\rm{t\;\delta }}\left( {{\rm{t}} - {\rm{a}}} \right)} \right] + {\rm{u}}\left( {\rm{t}} \right) - {\rm{u}}\left( {{\rm{t}} - {\rm{a}}} \right)\)

\(\frac{{dx\left( t \right)}}{{dt}} = \left[ {{\rm{t}}{{\left. \right|}_{{\rm{t}} = 0{\rm{\;}}}}{\rm{\delta }}\left( {\rm{t}} \right) - {\rm{t}}{{\left. \right|}_{{\rm{t}} = {\rm{a}}}}{\rm{\;\delta }}\left( {{\rm{t}} - {\rm{a}}} \right)} \right] + {\rm{u}}\left( {\rm{t}} \right)-{\rm{\;u}}\left( {{\rm{t\;}}-{\rm{\;a}}} \right)$\)

\(\frac{{dx\left( t \right)}}{{dt}} = \left[ {0 - {\rm{a\;\delta }}\left( {{\rm{t}} - {\rm{a}}} \right)} \right] + {\rm{u}}\left( {\rm{t}} \right) - {\rm{u}}\left( {{\rm{t\;}}-{\rm{\;a}}} \right)\)

\(\frac{{dx\left( t \right)}}{{dt}} = {\bf{u}}\left( {\bf{t}} \right) - {\bf{u}}\left( {{\bf{t}} - {\bf{a}}} \right) - {\bf{a}}\;{\bf{\delta }}\left( {{\bf{t}} - {\bf{a}}} \right)\)

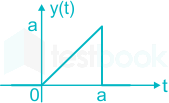
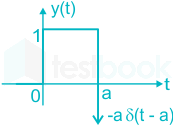
What is the power of the signal x(t) = 8 sin(2πt) + 4 sin(4πt)?

1. 40
2. 8
3. 32
4. 24

Answer (Detailed Solution Below)

Option 1 : 40

Concept:

Power of sinusoidal signal is given by:

\(P = \frac{{A_C^2}}{2}\)

The given signal consists of two sine signals.

Since Power is additive in nature

P_t = P₁ + P₂

\({P_t} = \frac{{A_{{C_1}}^2}}{2} + \frac{{A_{{C_2}}^2}}{2}\)

Calculation:

\({P_t} = \frac{{{8^2}}}{2} + \frac{{{4^2}}}{2}\)

P_t = 32 + 8 = 40 W

Inverse Fourier Transform of δ(ω - ω₀) is ______.

1. \(\frac{2π}{e^{jω_0}t}\)
2. \(e^{jω_0t}\)
3. \(\frac {e^{jω_0t}}{2\pi}\)
4. \(2\pi e^{jω_0t}\)

Answer (Detailed Solution Below)

Option 3 : \(\frac {e^{jω_0t}}{2\pi}\)

Concept:

Time-shifting property of Fourier transform:

If X(ω) is the Fourier transform of x(t),

\(x\left( {t - {t_0}} \right) ↔ X\left( \omega \right){e^{ - j\omega {t_0}}}\)  ---(1)

Duality property of Fourier transform:

If X(ω) is the Fourier transform of x(t),

\(X\left( t \right) ↔ 2\pi x\left( { - \omega } \right)\)

Calculation:

Fourier Transform of δ(t) = 1

Now by definition of inverse Fourier transform

\(\delta(\omega)\leftrightarrow \frac{1}{2\pi}\)

Now using time-shifting property from equation (1)

\(\delta(\omega \ - \ \omega_o)\leftrightarrow\frac{1}{2\pi}e^{j\omega_ot}\)

Hence option  (3) is the correct answer.

Important Points

Unit Impulse function:

A continuous-time unit impulse function δ(t), also called a Dirac delta function is defined as:

δ (t) = ∞ , t = 0

= 0,  otherwise

The unit impulse function is represented by an arrow with the strength of  '1' which represents its area.

\(\mathop \smallint \limits_{ - \infty }^\infty δ \left( t \right)dt = 1\)

Properties of Delta function:

Scaling Property:

\(δ \left( {at} \right) = \frac{1}{{\left| {at} \right|}}δ \left( t \right)\)

Multiplication Property:

X(t).δ(t – t0) = x(t0)δ(t – t0)

Sampling Property:

\(\mathop \smallint \limits_{ - \infty }^\infty x\left( t \right)δ \left( {t - {t_0}} \right)dt = x\left( {{t_0}} \right)\)

Important Expressions:

 X(t).δ(t) = x(0)δ(t)

\(\mathop \smallint \limits_{ - \infty }^\infty x\left( t \right)δ \left( t \right)dt = x\left( 0 \right)\)

A system is given by\(x\left( t \right) = {e^{at}}u\left( t \right)\). The system is

1. Causal and Stable
2. Non-causal and Stable
3. Causal and Unstable
4. Non-causal and Unstable

Answer (Detailed Solution Below)

Option 3 : Causal and Unstable

Causality:

1) For a causal system, the impulse response  of the system must use only the present and past values of the input to determine the output.

2) This requirement is a necessary and sufficient condition for a system to be causal, regardless of linearity.

​ Definition 1:  A system mapping x to y is causal if and only if, for any pair of input signals x₁(t),x₂(t) and any choice of t₀, such that:

x₁(t) = x₂(t), ∀ t < t₀

The corresponding output will satisfy:

y₁(t) = y₂(t), ∀ t < t₀

Definition 2:Suppose h(t) is the impulse response of any system 'H', The system is causal only if:

\(h\left( t \right) = 0,\;∀ \;t < 0\), otherwise, it is non-causal.

Stability:

If a system is BIBO stable, then the output will be bounded for every input to the system that is bounded.

\(\mathop \smallint \limits_{ - \infty }^{ + \infty } \left| {h\left( t \right)} \right|dt = h\left( t \right)\; < \infty \)

Analysis:

Given signal is \(x\left( t \right) = {e^{at}}u\left( t \right)\)

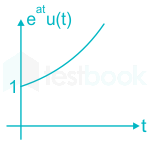
From the above figure, we can observe that:

1)  For, t < 0, x(t) = 0

2)  As time 't' tends to infinity, the response x(t) tends to infinity.

So, the signal is causal and unstable.

In analog communication, a unit impulse response of a causal system is ______ for t < 0.

1. 0
2. 1
3. infinite
4. -1

Answer (Detailed Solution Below)

Option 1 : 0

Explanation:

Causality:

1) For a causal system, theimpulse response of the system must use only the present and past values of the input to determine the output.

2) This requirement is a necessary and sufficient condition for a system to be causal, regardless of linearity.

​ Definition 1: A system mapping x to y is causal if and only if, for any pair of input signals x1(t),x2(t) and any choice of t0, such that:

\({x_1}\left( t \right) = {x_2}\left( t \right)\;,\;\forall \;t < {t_0}\)

The corresponding output will satisfy:

\({y_1}\left( t \right) = {y_2}\left( t \right)\;,\;\forall \;t < {t_0}\)

Definition2:Suppose h(t) is the impulse response of any system 'H', The system is causal only if:

\(h\left( t \right) = 0,\;\forall \;t < 0\), otherwise, it is non-causal.

Hence option (1) is the correct answer.

Example:

Given signal is\(x\left( t \right) = {e^{at}}u\left( t \right)\)

From the above figure, we can observe that:

1)  For, t < 0, x(t) = 0

2)  As time 't' tends to infinity, the response x(t) tends to infinity.

So, the signal is causal and unstable.

Important Points

Stability:

If a system is BIBO stable, then the output will be bounded for every input to the system that is bounded.

\(\mathop \smallint \limits_{ - \infty }^{ + \infty } \left| {h\left( t \right)} \right|dt = h\left( t \right)\; < \infty \)

Which of the following is not a standard input test signal?

1. Impulse signal
2. Ramp signal
3. Step signal
4. Speech signal

Answer (Detailed Solution Below)

Option 4 : Speech signal

Explanation:

The standard input test signals are mentioned below:

Unit impulse signal:

It is defined as a pulse compressed along the horizontal axis and stretched along the vertical axis keeping the area unity.

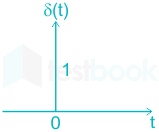
It is defined as,

\(\delta \left( t \right) = \left\{ {\begin{array}{*{20}{c}} {\infty ,\;\;t = 0}\\ {0,\;\;t \ne 0} \end{array}} \right.\)

It exists only at t= 0 and the area under impulse function is unity.

Hence for a system subjected to shock inputs, an Impulse function will be a good test signal.

Ramp input:

It is a standard input signal that consists of a constant rate of change in input.

The ramp is a signal, which starts at a value of zero and increases linearly with time

\(r\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {At;t \ge 0}\\ {0;else\;where} \end{array}} \right.\)

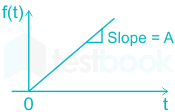
If amplitude A=1, it is called Unit Ramp Input.

If the inputs to control systems are gradually changing functions of time, then aramp function can be a good test signal.

Unit step signal  is represented as shown:

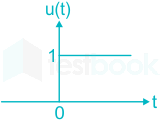
\(u\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {1,\;\;\;t > 0}\\ {0,\;\;\;t < 0} \end{array}} \right\}\)

0 to 1 jumps undefined. But mathematicallywe defineu(0) = ½

If a system is subjected to sudden disturbances, astep function will be a good test signal.

Speech Signal:

The speech signal, as it emerges from a speaker's mouth, nose, and cheeks, is a one-dimensional function (air pressure) of time. Microphones convert the fluctuating air pressure into electrical signals, voltages, or currents, in which form we usually deal with speech signals in speech processing.

Hence speech signal is not a standard input test signal

Important Points

Standard signal functions	Integral of standard signal
Impulse function - δ(t)	Step function - u(t)
Step function - u(t)	Ramp function - r(t)
Ramp function - r(t)	Parabolic function - p(t)

If the input x(t) and output y(t) of a system are related as y(t) = max (0, x(t)), then the system is

1. linear and time-invariant
2. linear and time-variant
3. non-linear and time-variant
4. non-linear and time-invariant

Answer (Detailed Solution Below)

Option 4 : non-linear and time-invariant

Concept:

Linearity: Necessary and sufficient condition to prove the linearity of the system is that the linear system follows the laws of superposition i.e. the response of the system is the sum of the responses obtained from each input considered separately.

y{ax1[t] + bx2[t]} = a y{x1[t]} + b y{x2[t]}

Conditions to check whether the system is linear or not.

• The output should be zero for zero input.
• There should not be any non-linear operator present in the system.

Time-Invariance: If the input to a time-invariant system is shifted in time, its output remains the same signal, but is shifted equally in time.

If the output for an input x(t) is y(t), then a time shift of t0 in the input gives the t0 shift in the output.

x(t) → y(t), then x(t – t0) → y(t – t0)

Application:

Given y(t) = max (0, x(t))

\(y(t)= \left\{ {\begin{array}{*{20}{c}} {0,\;\;\;\;x(t) < 0}\\ {x(t),x(t) > 0} \end{array}} \right.\)

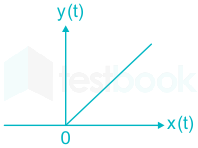
Linearity checking:

For input x₁(t) = -1 , Output y₁(t) = 0

For input x₂(t) = 1 , Output y₂(t) = 1

y(x1(t) + x2(t)) = y(-1 + 1) = y(0) = 0

y1(t) + y2(t) = 0 + 1 = 1

⇒ y(x1(t) + x2(t)) ≠ y1(t) + y2(t)

Hence the system is non linear.

Time-invariance checking:

Let the output is delayed by t_o

\(y(t-t_o)= \left\{ {\begin{array}{*{20}{c}} {0,\;\;\;\;\;\;\;\;\;\;\;x(t-t_o) < 0}\\ {x(t-t_o),x(t-t_o) > 0} \end{array}} \right.\)

Let the output of the system be g(t) for a delayed input x(t - t_o)

\(y_1(t)= \left\{ {\begin{array}{*{20}{c}} {0,\;\;\;\;g(t) < 0}\\ {g(t),g(t) > 0} \end{array}} \right.\\\;\\= \left\{ {\begin{array}{*{20}{c}} {0,\;\;\;\;\;\;\;\;\;\;\;x(t-t_o) < 0}\\ {x(t-t_o),x(t-t_o) > 0} \end{array}} \right.\\\;\\=y(t-t_o)\)

Hence, the given system is time-invariant

Identify the signal x(2t - 3) given x(t) as

Answer (Detailed Solution Below)

Option 2 :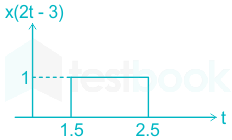

Concept:

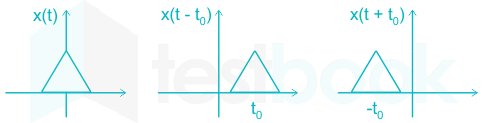
Time-shifting property: When a signal is shifted in the time domain it is said to be delayed or advanced based on whether the signal is shifted to the right or left.

For example:

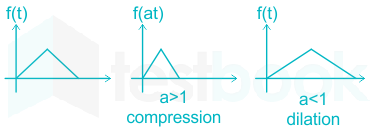
Time scaling property: A signal is scaled in the time domain with the scaling factor 'a'.

If a > 1, then the signal is contracted by a factor of 'a' along the time axis.

if a < 1, then the signal is expanded by a factor of 'a' along the time axis.

For example:

Analysis:

Whenever there is a combination of operations care should be taken while following the sequence of operations.

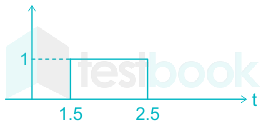
Correct approach:

x[2(t - 1.5)]

First, time scale the signal by factor 2.

Then, time shift the signal by 1.5

Incorrect approach:

x[2(t - 1.5)]

First, time shift the signal by 1.5

Then, time scale the signal by 2.

or,

Correct approach:

x[2t - 3]

First, time shift the signal by 3.

Then, time scale the signal by 2

Incorrect approach:

x[2t - 3]

First, time scale the signal by 2

Then, time shift the signal by 3.

In which system does the output at present instant depends on past inputs and outputs?

1. Invertible systems
2. Dynamic systems
3. Static systems
4. Linear systems

Answer (Detailed Solution Below)

Option 2 : Dynamic systems

Static and Dynamic Systems:

The static system is memory-less, i.e. the output depends only on the present input values.

Whereas a dynamic system is a memory system, i.e. the output at present instant depends on past inputs and outputs.

Example 1:y(t) = 2 x(t)

For present value t = 0, the system output is y(0) = 2x(0). Here, the output is only dependent upon the present input. Hence the system is memoryless or static.

Example 2: y(t) = 2 x(t) + 3 x(t-3)

For present value t=0, the system output is y(0) = 2x(0) + 3x(-3).

Here x(-3) is past value for the present input for which the system requires memory to get this output. Hence, the system is a dynamic system.

Linear and Nonlinear System:

Linearity: Necessary and sufficient condition to prove the linearity of the system is that the linear system follows the laws of superposition i.e. the response of the system is the sum of the responses obtained from each input considered separately.

y{ax1[n] + bx2[t]} = a y{x1[n]} + b y{x2[n]}

Conditions to check whether the system is linear or not.

1) The output should be zero for zero input

2) There should not be any non-linear operator present in the system

Invertible and Noninvertible System:

If the output is uniquely reproduced by input, then it called invertibility.

Example: y(t) = x2(t)

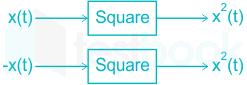
Two different input produces the same output. So, the system is non-invertible.

Signals and Systems Exam Questions and Solutions

Source: https://testbook.com/objective-questions/mcq-on-introduction-to-signals-and-systems--5eea6a0839140f30f369d726

Share :